AHSMC-2024-II-P4

Enunciado

Unha clase de $b+g>2$ estudantes, consistente en $b$ rapaces e $g$ rapazas, colócanse en círculo. Proba o seguinte:

1. Se $b=g=5$, entón hai un ou unha estudante que ten como veciñas a dúas rapazas.
2. Se $b+g$ é non divisíbel por 4, entón hai un ou unha estudante cuxos veciños son ou dous rapaces ou dúas rapazas.

---

Resolución

Solución

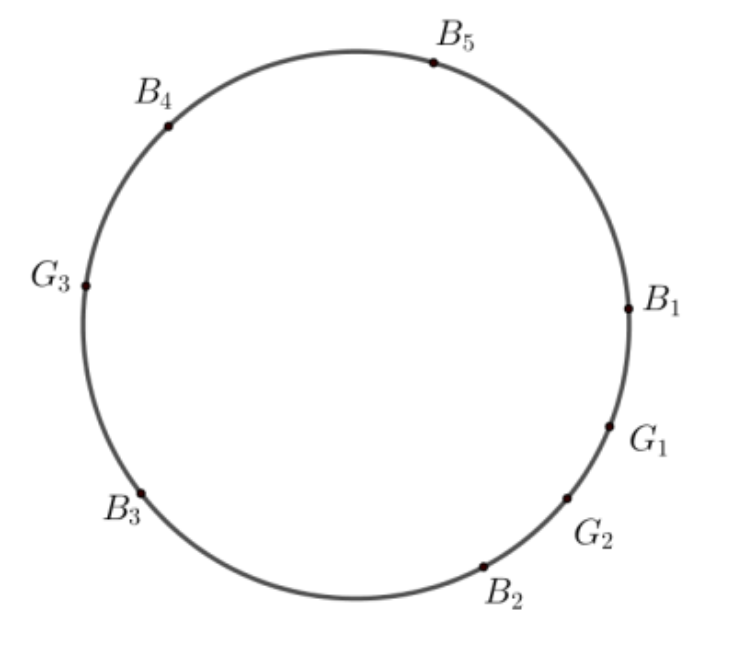
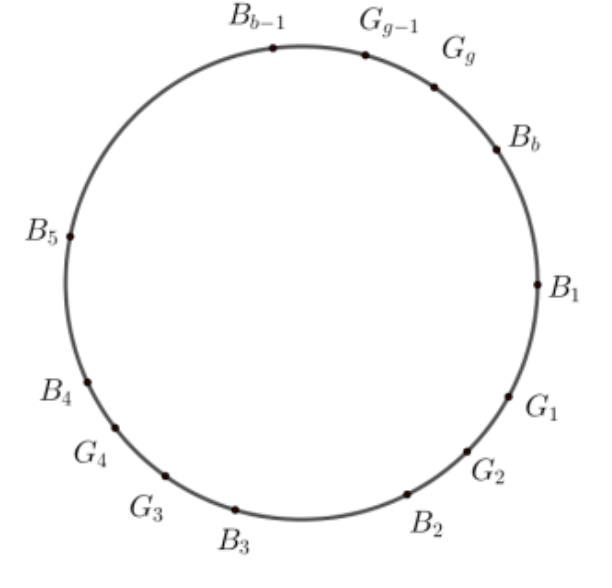
1. Consideremos os seguintes puntos dunha circunferencia, onde as rapazas son $G_1,G_2,...,G_g$ e os rapaces $B_1,B_2,...,B_b$, onde se representan no sentido das agullas do reloxo as posicións, onde $G_1\in \stackrel{⌢}{B_1{B}_2}$ Considerando o seguinte debuxo, asumindo que non existe ningún estudante con ambas veciñas rapazas:

Esta situación non pode ocurrir se tres rapazas están no mesmo arco $\stackrel{⌢}{B_i{B}_{i+1}}$ con $i=\mathrm{1...4}$ ou se polo menos unha rapaza está no arco $\stackrel{⌢}{B_5{B}_1}$. Analizaremos dous casos:

• Se $G_2\in \stackrel{⌢}{B_1{B}_2}$, entón $G_3\in \stackrel{⌢}{B_3{B}_4}$ e tamén $G_4$ ten que estar no arco $\stackrel{⌢}{B_3{B}_4}$: o cal leva a non ter ningunha posición para $G_5$
• Se $G_2\in \stackrel{⌢}{B_3{B}_4}$, entón $G_3$ ten que estar tamén no arco $\stackrel{⌢}{B_3{B}_4}$, pero neste escenario non hai posicións para $G_4$ e $G_5$

1. Asumindo que non hai ningún estudante cuxos veciños son só rapazas ou rapaces, a cal non pode pasar se hai polo menos tres rapazas no mesmo arco $\stackrel{⌢}{B_i{B}_{i+1}}$ con $i=1,...,b-1$, ou se unha rapaza está no arco $\stackrel{⌢}{B_b{B}_1}$. Entón, debemos ter $G_2\in \stackrel{⌢}{B_1{B}_2}$; $G_3,G_4\in \stackrel{⌢}{B_3{B}_4}$; …, $G_{g-1},G_g\in \stackrel{⌢}{B_{b-1}{B}_b}$. Así, consecuentemente, $g=b=2k$, sendo $g+b$ divisíbel por 4, o cal é unha contradición.

---

Dúbidas & Comentarios

Nesta sección pódesnos deixar as túas dúbidas e comentarios a cerca do problema anterior. Non teñas teima en preguntar, estamos aí para botar unha man!