AMO-2015-I-P2

Enunciado

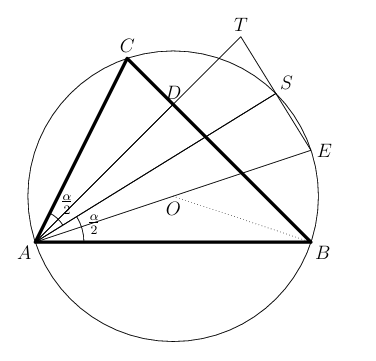
Sexa $ABC$ un triángulo acutángulo con $AC<AB$ inscrito nunha circunferencia de radio $R$. Sexa $D$ o pé da altura dende $A$ en $BC$ e sexa $T$ o punto da liña $AD$ onde $AT=2R$, tal que $D$ quede entre $A$ e $T$. Finalmente sexa $S$ o punto medio do arco $BC$ na circunferencia que non inclúe a $A$. Proba que $\angle AST=90^{\circ }$

---

Resolución

Solución

Como é habitual, imos denotar os ángulos $\angle BAC$, $\angle ABC$ e $\angle BCA$ por $\alpha ,\beta$ e $\gamma$ respectivamente, e o centro da circunferencia coma $O$. Por hipótese, temos $\beta <\gamma$. Sexa $E$ o punto da circunferencia de $ABC$ diametralmente oposto a $A$. Polo teorema do ángulo inscrito, temos $\angle AOB=2\gamma$. Por definición, $S$ é a intersección da bisectriz de $\angle CAB$ e a circunferencia. Notemos que: $\angle EAS=\angle BAS-\angle BAO=\frac{\alpha }{2}-\frac{1}{2}(180^{\circ }-\angle AOB)=$ $=\frac{\alpha }{2}-\frac{1}{2}(180^{\circ }-2\gamma )=\frac{\alpha }{2}+\gamma -90^{\circ }$ Como tamén temos: $\angle SAT=\angle SAC-\angle DAC=\frac{\alpha }{2}-(90^{\circ }-\angle ACD)=\frac{\alpha }{2}+\gamma -90^{\circ }$ Polo que $\angle EAS=\angle TAS$. Como tamén temos $AE=AT=2R$, os triángulos $ASE$ e $AST$ son congruentes e así, $\angle AST=\angle ASE$. Como $AE$ é o diámetro dunha circunferencia e temos $\angle ASE=90^{\circ }$, temos a proba.

---

Dúbidas & Comentarios

Nesta sección pódesnos deixar as túas dúbidas e comentarios a cerca do problema anterior. Non teñas teima en preguntar, estamos aí para botar unha man!