IGO-2017-Mid-P2

Enunciado

Sexan ${\omega }_1$ e ${\omega }_2$ dous círculos que se intersecan en $A$ e $B$ puntos distintos. Consideremos unha recta que pase por $B$ e que interseque a ${\omega }_1$, ${\omega }_2$ en $C$, $D$ respectivamente, con $C\ne D$. Sexan $E\in {\omega }_1$, $F\in {\omega }_2$ tal que $CE=CB$ e $BD=DF$. Supoñamos que $BF$ interseca ${\omega }_1$ en $P$, e $BE$ interseca ${\omega }_2$ en $Q$. Proba que $A,P,Q$ son colineais.

---

Resolución

Solución

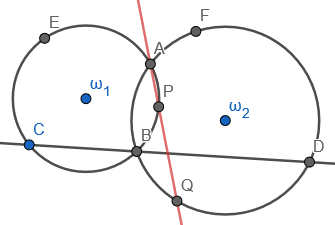
Vemos a configuración do problema:

Primeiro, cómpre decatarse de que probar que $A,P,Q$ son colineais e equivalente a probar que $\angle BAP=\angle BAQ$. Utilizaremos as propiedades dos cuadriláteros cíclicos para demostrar esta igualdade. Nótese que todos os puntos definidos no enunciado están sobre ${\omega }_1$ ou ben ${\omega }_2$, polo cal sempre teremos un cuadrilátero cíclico ao considerar catro puntos sobre un certo ${\omega }_i$ concreto.

Por como construímos $F$, sabemos que $BD=DF$, polo que $FBD$ e un triángulo isósceles e por tanto $\angle BFD=\angle DBF$. Por ángulos complementarios, temos que $\angle DBF=180^{\circ }-\angle CBP$. Como $ECBP$ é un cíclico, sabemos que os ángulos opostos son complementarios, polo que $\angle CBP+\angle CEP=180^{\circ }$. Concluímos que $\angle BFD=180^{\circ }-\angle CBP=\angle CEP$.

De forma similar, $ECB$ é un triángulo isósceles por como construímos $E$, polo que $\angle CEB=\angle CBE$. Por ángulos opostos sabemos que $\angle CBE=\angle QBD$. Como $BQDF$ é cíclico sabemos que un ángulo entre un lado e unha diagonal coincide co ángulo formado polo lado oposto e a outra diagonal, polo que $\angle QBD=\angle QFD$. Xuntando todas as congruencias de ángulos de este parágrafo, temos que $\angle CEB=\angle QFD$.

Por último, nótese que podemos reescribir $\angle BFD=\angle CEP$ como $\angle CEB+\angle BEP=\angle BFQ+\angle QFD$, e tendo en conta que $\angle CBE=\angle QFD$ concluímos que $\angle BEP=\angle BFQ$. Agora ben, como $EBPA$ e $ABQF$ son cíclicos entón $\angle BAP=\angle BEP$ e $\angle BFQ=\angle BAQ$, respectivamente. Por ende $\angle BAP=\angle BAQ$, tal como queríamos demostrar.

Podedes xogar con esta configuración en: https://www.geogebra.org/m/ajpcqvdq.

---

Dúbidas & Comentarios

Nesta sección pódesnos deixar as túas dúbidas e comentarios a cerca do problema anterior. Non teñas teima en preguntar, estamos aí para botar unha man!