OME-1973-P4

Enunciado

Sexan $C$ e $C^{\prime }$ dúas circunferencias concéntricas de radios $r$ e $r^{\prime }$ respectivamente. Determinar canto debe de valer o cociente $\frac{r^{\prime }}{r}$ para que a coroa limitada por $C$ e $C^{\prime }$ existan outro circunferencias $C_i$, con $i=1,\dots ,8$, que sexan tanxentes a $C$ e a $C^{\prime }$, e tamén que $C_i$ sexa tanxente a $C_{i+1}$ para $i=1,\dots ,7$ e $C_8$ tanxente a $C_1$.

---

Resolución

Pista

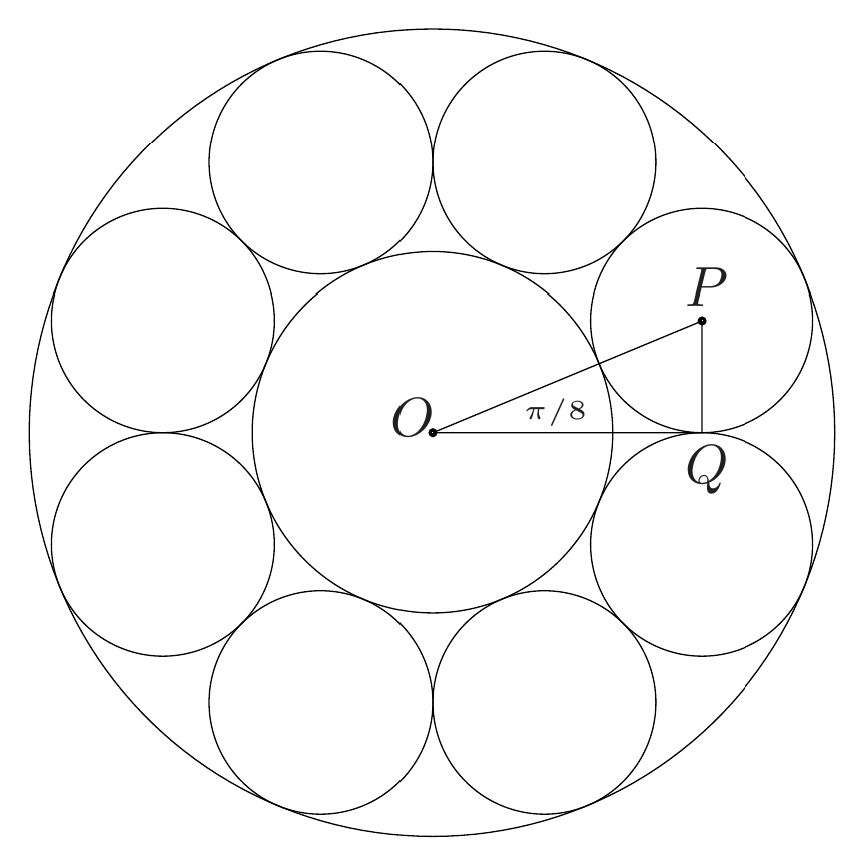
Considerar o triángulo formado polo centro $O$ de $C$ e $C^{\prime }$, o centro $P$ de unha das circunferencias $C_i$ e o punto $Q$ de tanxencia entre $C_i$ e $C_{i+1}$.

Solución

Vemos no seguinte debuxo a configuración do problema, no que $C$ está contida en $C^{\prime }$.

Vemos que podemos calcular $\overline{OP}$ e $\overline{PQ}$ como

$$\begin{array}{rl}\overline{OP}& =r+\frac{r^{\prime }-r}{2}=\frac{r+r^{\prime }}{2}.\\ \overline{PQ}& =\frac{r^{\prime }-r}{2}.\end{array}$$

Ademais, dada a configuración das oito circunferencias pequenas, sabemos que

$$\widehat{POQ}=\frac{\pi }{8}=22.5^{\circ }.$$

Entón pola definición do seno, temos que

$$\sin \frac{\pi }{8}=\frac{\frac{r^{\prime }-r}{2}}{\frac{r+r^{\prime }}{2}}=\frac{\frac{r^{\prime }}{r}-1}{1+\frac{r^{\prime }}{r}}.$$

Despexando, obtense a expresión buscada

$$\frac{r^{\prime }}{r}=\frac{1+\sin \frac{\pi }{8}}{1-\sin \frac{\pi }{8}}\approx \mathrm{2.24.}$$

---

Dúbidas & Comentarios

Nesta sección pódesnos deixar as túas dúbidas e comentarios a cerca do problema anterior. Non teñas teima en preguntar, estamos aí para botar unha man!