OME-1995-P3

Enunciado

Dado $G$ o baricentro dun triángulo $ABC$ debuxamos unha recta que pasa por el e que corta ao lado $AB$ no punto $P$ e ao lado $AC$ no punto $Q$. Proba que $\frac{PB}{PA}\cdot \frac{QC}{QA}\le \frac{1}{4}$.

---

Resolución

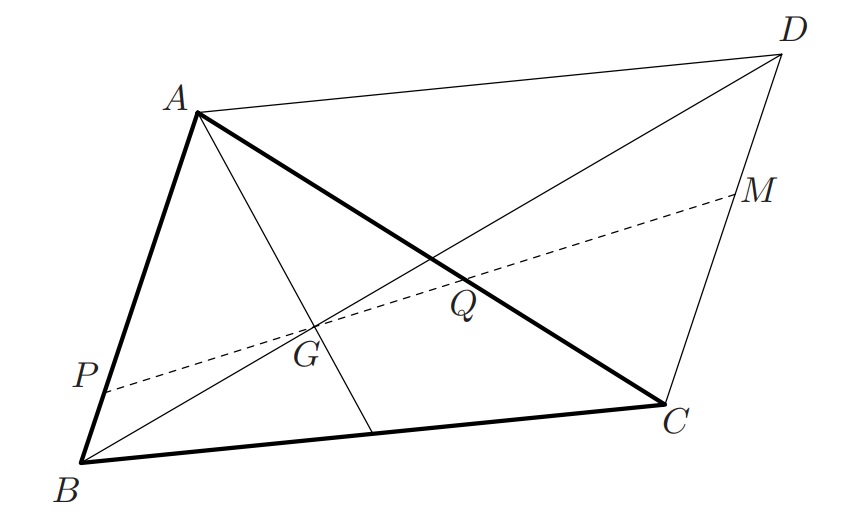
Solución $D$ ao vértice do ''novo'' triángulo, como na figura, e $M$ será o punto de corte entre a recta do enunciado, $PQ$ e o segmento $CD$. Por outra banda, imos tomar como unidade o lado $AB$, de xeito que se $x=PB$ entón $AP=1-x$. Os triángulos $AQC$ e $QMC$ son semellantes. Polo tanto, temos que: $\frac{QC}{QA}=\frac{MC}{AP}=\frac{MC}{1-x}$ Os triángulos $GPD$ e $GMB$ tamén son semellantes, polo que $\frac{PB}{MD}=\frac{GB}{GD}=\frac{1}{2},$ onde a derradeira igualdade dedúcese da propiedade de que o baricentro sitúase a 2/3 de distancia (lonxitude da mediana) do vértice e 1/3 do lado. Así, o baricentro está a 2/3 de $B$ e 4/3 de $D$. Polo tanto, $MD=2x$ e $MC=1-2x$. En consecuencia, probar a relación pedida no enunciado é equivalente a demostrar que $\frac{x(1-2x)}{(1-x{)}^2}\le \frac{1}{4}$. Ou equivalentemente $9x^2-6x+1\ge 0$, e isto é trivialmente certo. A igualdade veríficase se, e só se, $x=\frac{1}{3}$.

O primeiro paso é duplicar o triángulo, de xeito que obteñamos un paralelogramo no que os lados sexan dous do triángulo e a diagonal resulte o terceiro lado do triángulo orixinal, como se pode observar na figura. Chamaremos

---

Dúbidas & Comentarios

Nesta sección pódesnos deixar as túas dúbidas e comentarios a cerca do problema anterior. Non teñas teima en preguntar, estamos aí para botar unha man!