Enunciado
Sobre un taboleiro con forma de triángulo equilátero de filas (a figura sería ) xógase un solitario. Sobre cada casilla colócase unha ficha branca por un lado e negra polo outro. Inicialmente só unha ficha situada nun dos vértices ten o lado negro cara arriba, as demais teñen o lado branco cara arriba. En cada movemento do xogo se retira soamente unha ficha negra do taboleiro e se lle dá a volta a cada unha das fichas que ocupa unha casilla veciña (é dicir, ás que están unidas por un segmento). Despois de varios movementos, é posible quitar tódalas fichas do taboleiro?
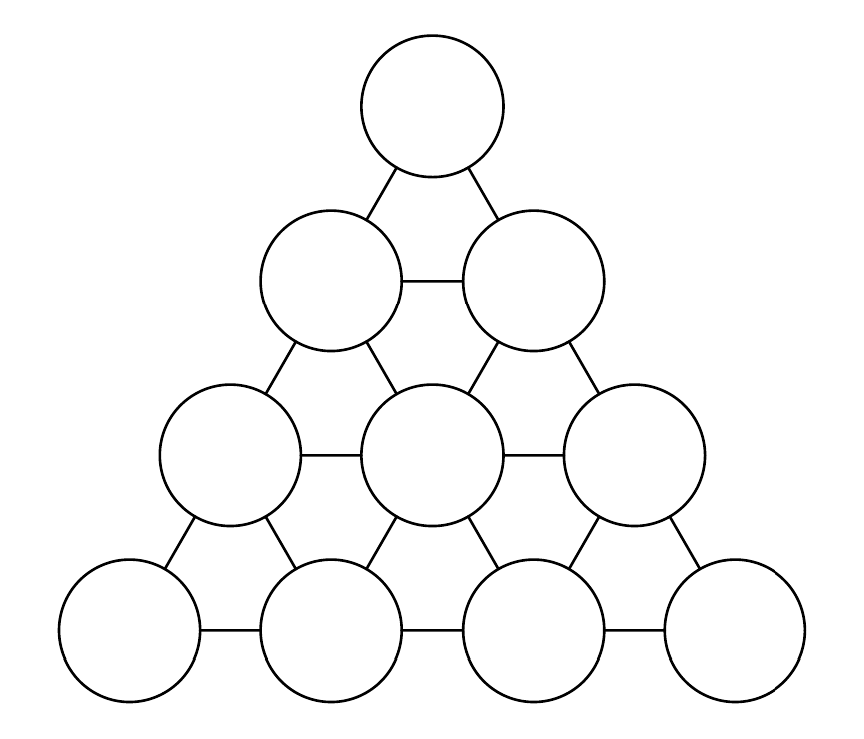
Resolución
Pista
Paridade e redución ao absurdo.
Solución
Non se pode. Procedemos por redución ao absurdo. Se se puidese, entón chegaría un punto no que teríamos unicamente unha ficha co lado negro cara arriba, mais isto non pode pasar xa que cada ficha que ten a parte branca cara arriba ao comezo está unida a un número par de fichas, polo tanto, se todas as fichas coas que está unida se quitan esta cambiará de color un número par de veces, volvendo ter a parte branca cara arriba.
Dúbidas & Comentarios
Nesta sección pódesnos deixar as túas dúbidas e comentarios a cerca do problema anterior. Non teñas teima en preguntar, estamos aí para botar unha man!

