NMC-35th-P4

Enunciado

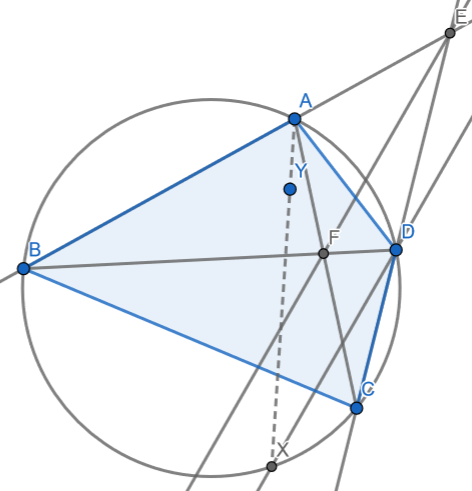
Sexan $A,B,C,D$ puntos nunha circunferencia $\omega$. Supoñamos que $AB$ e $CD$ intersecan nun punto $E$ e $BD$ e $AC$ intersecan en $F$. Sexa $X\ne D$ tal que $x\in \omega$ e $DX$ e $EF$ sexan paralelas. Por último, sexa $Y$ a reflexión de $D$ a través de $EF$.

• Demostra que $AYFE$ é un cuadrilátero cíclico.
• Demostra que $A,X,Y$ son colineais.

---

Resolución

Pista

Para o apartado (a), mira con coidado o debuxo (ou fai ti o teu propio) e aproveita o resultado típico de cuadrilátero cíclico. No apartado (b) intenta traducir a condición $A,X,Y$ son colineais en termos de ángulos, xa que ó dispor de cuadriláteros cíclicos coñocemos moitos ángulos. Para facer isto, lembra o primeiro exercicio que fixemos de cuadriláteros cíclicos.

Solución $ABCD$ é cíclico e queremos probar que $AYFE$ tamén o é, polo que parece ser boa idea intentar demostrar isto baseándonos en que $ABCD$ é cíclico.

Comecemos co apartado (a). Sabemos que

Obviamente queremos demostrar que $AYFE$ é cíclico a través dos seus ángulos ou semiángulos (xa que por agora non coñecemos ningunha outra forma), polo que debemos considerar ángulos tal que teñan relación directa cos ángulos de $ABCD$. Os vértices $E$ e $F$ non teñen relación directa con $ABCD$, polo que parece que a forma máis sinxela e traballar cos vértices $A$ e $Y$, xa que o primeiro pertence a $ABCD$ e o segundo relaciónase de forma directa co vértice $D$ dese cuadrilátero, xa que é a sua reflexión.

Tendo esta análise en conta, é directo ver que $AYFE$ é cíclico, xa que $\angle EAF=\angle EYF$. Isto é debido a que $\angle EAF=180^{\circ }-\angle CAB=180^{\circ }-\angle CDB=\angle FDE=\angle EYF,$ onde utilizamos que $\angle CAB=\angle CDB$ por ser $ABCD$ cíclico e que $Y$ é a reflexión de $D$ respecto a $EF$. Fagamos agora o seguinte apartado. É obvio que teremos que usar as relacións de ángulos que os cuadriláteros cíclicos proporcionan, pero temos o problema de que a priori a condición ‘A,X,Y son colineais’ non depende de ángulos, polo que temos que traducir a susodita condición de tal forma que dependa de algún ángulo. Agora ben, isto non é algo novedoso, xa que no primeiro exercicio de cuadriláteros cíclicos apareceu o mesmo problema. Facendo un pouco de memoria, podemos considerar a seguinte traducción: $X,Y\text{ colineais}⟺\angle BAY=\angle BAX.$ Demostrar agora esta condición consiste en aplicar repetidas veces as propiedades dos cuadriláteros cíclicos:

$$\begin{array}{rll}1.& \angle BAX=\angle BDX& ABCD\text{ eˊ cıˊclico}\\ 2.& \angle BDX=\angle FDX& \text{extendemos un lado do aˊngulo}\\ 3.& \angle FDX=\angle DFE& DX\text{ e }EF\text{ son paralelos}\\ 4.& \angle DFE=\angle EFY& Y\text{ eˊ a reflexioˊn de }D\text{ respecto a }EF\\ 5.& \angle EFY=180^{\circ }-\angle EAY& AYFE\text{ eˊ cıˊclico}\\ 6.& 180^{\circ }-\angle EAY=\angle BAY& \text{aˊngulos complementarios}\\ 7.& \angle BAX=\angle BAY& \text{debido a 1–6.}\end{array}$$

Nota: No apartado (b) poden usarse outras ‘traducións’. Nota 2: O enunciado deste exercicio foi lixeiramente modificado para facilitar a lectura. Omitíronse diversas condicións implícitas no debuxo dado, pero as cales deben ser consideradas se se quere estudar a situación xeral. O enunciado completo é: Sexan $A,B,C,D$ puntos nunha circunferencia $\omega$ tal que $ABCD$ é un cuadrilátero convexo. Supoñamos que $AB$ e $CD$ intersecan nun punto $E$ tal que $A$ está entre $B$ e $E$, e $BD$ e $AC$ intersecan en $F$. Sexa $X\ne D$ tal que $x\in \omega$ e $DX$ e $EF$ sexan paralelas. Por último, sexa $Y$ a reflexión de $D$ a través de $EF$ e supoñamos que $Y$ encóntrase no interior do círculo $\omega$. Demostra que $A,X,Y$ son colineais. Nota 3: Podes xogar con esta configuración no seguinte enlace: https://www.geogebra.org/m/zy7v9uxv.

---

Dúbidas & Comentarios

Nesta sección pódesnos deixar as túas dúbidas e comentarios a cerca do problema anterior. Non teñas teima en preguntar, estamos aí para botar unha man!